Geometric Identification of Points-of-Interest: Theory and Equations

Roshan Kamath, Vidyadhar Gurram
2015 Jun 05

Abstract

Given the GPS coordinates of a user, the orientation of their camera, and the linear distance to the Point-of-Interest (POI) being photographed, we determine the GPS coordinates of the POI. We derive the analytical expressions that relate the input data to the POI coordinates for the most general case. Approximate forms of the equations are also derived, in two different ways, for the more common case of the POI in the immediate neighbourhood of the user.

Acknowledgements

This work was done in my spare time while employed by Motorola Mobility LLC, Chicago, Illinois - 60654, USA. It has been reproduced on this blog after receiving the appropriate Motorola Mobility internal publication clearance. This 'problem' was obliquely borne out of discussions with Vidyadhar Gurram. I subsequently cast it into symbolic form and derived the pertinent equations.

1. Symbol glossary

Note: All distances are in metres and all angles are in radians. 'Sea level' is defined by the surface of the GPS reference ellipsoid.

Symbol	Description
$\lambda_u$	User's longitude $(0 \le \lambda_u \lt 2\pi)$
$\delta_u$	User's latitude $(-\pi/2 \lt \delta_u \lt \pi/2)$
$h_u$	User's height above sea level
$R_u$	Distance to the centre of the Earth from sea level at the user's position
$A$	Azimuth angle of the camera orientation measured due West  of North and valid only when $\delta_u \ne \pm\pi/2$ $(0 \le A \lt 2\pi)$
$z$	Zenith angle of the camera orientation $(0 \le z \le \pi)$
$r$	Euclidean straight line distance from the camera to the target  along the camera orientation vector
$\lambda_t$	Target's longitude $(0 \le \lambda_t \lt 2\pi)$
$\delta_t$	Target's latitude $(-\pi/2 \lt \delta_t \lt \pi/2)$
$h_t$	Target's height above sea level
$R_t$	Distance to the centre of the Earth from sea level at the target's position
$\alpha$	Angular separation between the user and the target as seen  from the centre of the Earth $(0 \le \alpha \le \pi)$
$\Delta\lambda$	$\lambda_t - \lambda_u$, the difference between the target and user longitudes
U	User (in figures)
T	Target (in figures)
N	North pole of the Earth (in figures)
C	Centre of the Earth (in figures)

2 Goal

Given the GPS coordinates ($\lambda_u$,$\delta_u$,$h_u$) of the user $U$, the orientation $(A,z)$ of the user's camera, and the distance $r$ to the target $T$ being photographed, determine the GPS coordinates ($\lambda_t$,$\delta_t$,$h_t$) of the target $T$.

Figure 2.1: Plane of the triangle $UTC$

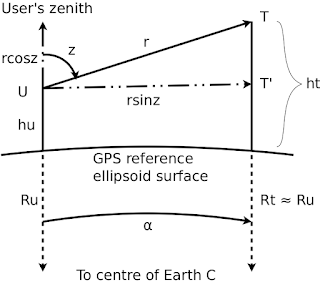
In figure 2.1 the user $U$ and target $T$ are at an altitude $h_u$ and $h_t$, respectively, above the GPS reference ellipsoid surface ('sea level'). Since the Earth is a geoid and not a perfect sphere, the distance to the centre of the Earth from the 'sea level' is taken to be $R_u$ and $R_t$ respectively. The orientation of the user's camera is defined by the vector $\overrightarrow{UT}$ whose length is $r$ and whose zenith angle is $z$. The angle subtended at the centre of mass of the Earth by $U$ and $T$ is denoted $\alpha$.

Figure 2.2: Projections on the Celestial Sphere

Figure 2.2 shows the projections of $U$ and $T$ onto the Celestial Sphere. The angle between the planes of the two great arcs $\widehat{NU}$ and $\widehat{NT}$ is the difference in the longitude, $\Delta\lambda$ (= $\lambda_t - \lambda_u$), between $U$ and $T$. The arc $\widehat{NU}$ represents the co-latitude, $\frac{\pi}{2}-\delta_u$, of the user; similarly $\widehat{NT}$ represents $\frac{\pi}{2}-\delta_t$. The arc $\widehat{UT}$ represents $\alpha$ (from figure 2.1). $\angle{NUT}$ (= $\angle{A}$) is the azimuth angle (measured due West of North) of the orientation vector $\overrightarrow{UT}$ (from figure 2.1).

3 Computation of the target's coordinates

3.1 Analytical Expressions

The law of cosines on $\Delta{CUT}$ in figure 2.1 gives,

$$(R_t+h_t)^2 = r^2 + (R_u+h_u)^2 - 2r(R_u+h_u)\cos(\pi-z)$$

i.e.,

$$\begin{align}(R_t+h_t)^2 =\ & r^2 + (R_u+h_u)^2 \nonumber \\ &+ 2r(R_u+h_u)\cos(z)\label{eq:3.1}\end{align}$$

where $r$, $R_u$, $h_u$, and $z$ are known ($R_u$ is calculated from $\delta_u$ and the GPS reference ellipsoid (section 6)). This gives $(R_t+h_t)$.

Similarly,

$$\begin{align}r^2 =\ &(R_u+h_u)^2 + (R_t+h_t)^2 \nonumber \\ &- 2(R_u+h_u)(R_t+h_t)\cos(\alpha)\label{eq:3.2}\end{align}$$

where $r$, $R_u$, $h_u$, and $(R_t+h_t)$ are known. This gives $\cos(\alpha)$ and hence $\alpha$.

The cosine rule for spherical triangles on $\Delta{NUT}$ in figure 2.2 gives

$$\cos(\frac{\pi}{2}-\delta_t) = \cos(\frac{\pi}{2}-\delta_u)\cos(\alpha) + \sin(\frac{\pi}{2}-\delta_u)\sin(\alpha)\cos(A)$$

i.e.,

$$\begin{equation}\label{eq:3.3}\sin(\delta_t) = \sin(\delta_u)\cos(\alpha) + \cos(\delta_u)\sin(\alpha)\cos(A)\end{equation}$$

where $\delta_u$, $\alpha$, and $A$ are known. This gives $\sin(\delta_t)$ and hence $\delta_t$.

The sine rule for spherical triangles on $\Delta{NUT}$ in figure 2.2 gives

$$ \frac{\sin(\Delta\lambda)}{\sin(\alpha)} = \frac{\sin(A)}{\sin(\frac{\pi}{2}-\delta_t)} \quad \text{provided } \delta_t \ne \pm\pi/2$$

i.e.,

$$\begin{equation}\label{eq:3.4}\sin(\Delta\lambda) = \frac{\sin(\alpha)\sin(A)}{\cos(\delta_t)}\quad\text{for}\ \delta_t \ne \pm\pi/2\end{equation}$$

where $\alpha$, $A$, and $\delta_t$ are known. This gives $\Delta\lambda$ and hence $\lambda_t\ (=\lambda_u+\Delta\lambda)$.

3.2 Algorithm

1. Acquire $\lambda_u$, $\delta_u$, and $h_u$ from location services (e.g. GPS).
2. Acquire $A$ and $z$ from the geomagnetic field and gravity sensors, or equivalent sources.
3. Acquire $r$ from the camera (if possible) or a range-finder accessory.
4. Compute $R_u$ using $\delta_u$ and the GPS reference ellipsoid (section 6).
5. Compute $R_t + h_t$ using equation ($\ref{eq:3.1}$).
6. Compute $\cos(\alpha)$ using equation ($\ref{eq:3.2}$). Then compute $\sin(\alpha)$. Note that $0 \le \alpha \le \pi$ and $\sin(\alpha)$ is non-negative. 
7. Compute $\sin(\delta_t)$ using equation ($\ref{eq:3.3}$). Then compute $\cos(\delta_t)$ and $\delta_t$. Note that $-\pi/2 \lt \delta_t \lt \pi/2$ and the sign of $\delta_t$ is determined by that of $\sin(\delta_t)$.
8. Compute $\sin(\Delta\lambda)$ using equation ($\ref{eq:3.4}$). Then compute $\Delta\lambda$. Note that $\Delta\lambda$ is positive if $0 \lt A \lt \pi$, negative if $\pi \lt A \lt 2\pi$, and $0$ if $A = 0 \text{ or } \pi$.
9. Compute $\lambda_t = \lambda_u + \Delta\lambda$.
10. Compute $R_t$ using $\delta_t$ and the GPS reference ellipsoid (section 6).
11. Compute $h_t$ by subtracting $R_t$ from $(R_t+h_t)$.

The coordinates of the target are thus determined to be ($\lambda_t$, $\delta_t$, $h_t$).

4 Initial order approximations

For the most common cases, where the user and the target are situated relatively close to each other (i.e. $|\alpha| \ll 1$), approximations can be employed for faster computational purposes.

The full set of initial order approximations is:

$$\begin{align}h_t &\approx h_u + r\cos z \label{eq:4.1}\\ \alpha &\approx \frac{r\sin z}{(R_u+h_u)} \label{eq:4.2}\\\delta_t &\approx \delta_u + \alpha \cos A \label{eq:4.3}\\ \lambda_t &\approx \lambda_u + \frac{\alpha\sin A}{\cos\delta_u}\quad\text{for}\ \delta_u \ne\pm\pi/2 \label{eq:4.4}\end{align}$$

where $R_u$, the distance to the centre of the Earth from 'sea level' at the user's location, must be first determined from $\delta_u$ and the GPS reference ellipsoid (section 6). The derivation of the above approximations can be done in two ways as follows.

4.1 The quick and dirty derivation

For very small angles and short distances (compared to the semi-major axis of the Earth), spherical triangles can be approximated by plane triangles, and arcs can be approximated by straight line segments. See corresponding figures 4.1 and 4.2. We use $R_t \approx R_u$ so that all unknown quantities are expressed in terms of known ones ($\lambda_u$, $\delta_u$, $h_u$, $A$, $z$, $r$, $R_u$).

Figure 4.1: Plane of the triangle $UTC$ for very small $\alpha$

Figure 4.2: Projections on the Celestial Sphere for very small $\alpha$

The orientation vector of length $r$ can be decomposed into two components. The vertical component is $r\cos z$ while the horizontal component is $r\sin z$.

The difference in elevation between the user and the target, $h_t - h_u$, is approximated by the vertical component, $r\cos z$, of the orientation vector. Thus,

$$h_t \approx h_u + r\cos z $$

which is equation ($\ref{eq:4.1}$).

The 'horizontal distance' between the user and the target, $\alpha(R_u+h_u)$, is approximated by the horizontal component, $r\sin z$, of the orientation vector. Thus,

$$\alpha \approx \frac{r\sin z}{(R_u+h_u)}$$

which is equation ($\ref{eq:4.2}$).

The horizontal distance between the user and the target, $\alpha(R_u+h_u)$, can itself be decomposed into two components. The component along the North-South axis is $\alpha(R_u+h_u)\cos A$ which approximates the difference in latitude measured as a distance at the longitude of the user, i.e. $(R_u+h_u)(\delta_t-\delta_u)$. Thus,

$$\delta_t \approx \delta_u + \alpha\cos A$$

which is equation ($\ref{eq:4.3}$).

Similarly, the component along the East-West axis is $\alpha(R_u+h_u)\sin A$ which approximates the difference in longitude measured as a distance at the latitude of the user, i.e. $\Delta\lambda(R_u+h_u)\cos\delta_u$ provided $\delta_u \ne \pm\pi/2$. Thus,

$$\Delta\lambda \approx \frac{\alpha\sin A}{\cos\delta_u} \quad \text{for } \delta_u \ne \pm\pi/2$$

or

$$\lambda_t \approx \lambda_u + \frac{\alpha\sin A}{\cos\delta_u} \quad \text{for } \delta_u \ne \pm\pi/2$$

which is equation ($\ref{eq:4.4}$).

4.2 The analytical derivation

We have $R_t \approx R_u$ and $h_u \ll R_u$, $h_t \ll R_u$, and $r \ll R_u$ so that we can neglect second order terms in $\frac{h_u}{R_u}$, $\frac{h_t}{R_u}$, and $\frac{r}{R_u}$. Equation ($\ref{eq:3.1}$) then becomes

$$\begin{align*}(R_u + h_t)^2 &\approx r^2 + (R_u + h_u)^2 +2r(R_u + h_u)\cos(z)\\ R_u^2(1 + \frac{h_t}{R_u})^2 &\approx r^2 + R_u^2(1+\frac{h_u}{R_u})^2 + 2r(R_u + h_u)\cos(z)\\ (1 + \frac{h_t}{R_u})^2 &\approx (1+\frac{h_u}{R_u})^2 + \frac{2r\cos(z)}{R_u}\\ (1+2\frac{h_t}{R_u}) &\approx (1 + 2\frac{h_u}{R_u}) + \frac{2r\cos z}{R_u}\end{align*}$$

or

$$h_t \approx h_u + r\cos z$$which is equation ($\ref{eq:4.1}$).

The other equations yield $\alpha \approx 0$, $\delta_t \approx \delta_u$, and $\Delta\lambda \approx 0$ which are trivially correct and vacuous. These values are thus sensitive to second order terms.

Substituting $R_t \approx R_u$ and equation ($\ref{eq:4.1}$) into equation ($\ref{eq:3.2}$) gives

$$\begin{align*}r^2 \approx\ &(R_u+h_u)^2 + (R_u+h_u+r\cos z)^2\\ &- 2 (R_u+h_u)(R_u+h_u+r\cos z)\cos\alpha\\ =\ &2(R_u+h_u)^2 + 2(R_u+h_u)(r\cos z) + (r\cos z)^2\\ &- 2(R_u+h_u)^2\cos\alpha - 2(R_u+h_u)(r\cos z)\cos\alpha\\ =\ &2(R_u+h_u)^2(1-\cos\alpha)\\ &+ 2(R_u+h_u)(r\cos z)(1-\cos\alpha) + (r\cos z)^2\end{align*}$$

or

$$\begin{align*}(r\sin z)^2 &\approx 2(R_u+h_u)(1-\cos\alpha)(R_u+h_u+r\cos z)\\ &= 2(R_u+h_u)(R_u+h_u+r\cos z)(2\sin^2(\frac{\alpha}{2}))\end{align*}$$

i.e.,

$$\begin{align*}\sin^2(\frac{\alpha}{2}) &\approx \frac{(r\sin z)^2}{4(R_u+h_u)(R_u+h_u+r\cos z)}\\ &= \frac{(r\sin z)^2}{4(R_u+h_u)^2(1+\frac{r\cos z}{R_u+h_u})}\\ &\approx \frac{(r\sin z)^2}{4(R_u+h_u)^2}(1-\frac{r\cos z}{R_u+h_u})\\ &\approx \frac{(r\sin z)^2}{4(R_u+h_u)^2}\end{align*}$$

i.e.,

$$\sin(\frac{\alpha}{2}) \approx \frac{r\sin z}{2(R_u+h_u)}$$

or

$$\frac{\alpha}{2} \approx \frac{r\sin z}{2(R_u+h_u)} \quad \text{as } |\alpha| \ll 1 \\$$

Thus

$$\alpha \approx \frac{r\sin z}{(R_u+h_u)}$$

which is equation ($\ref{eq:4.2}$).

Using $|\alpha| \ll 1$ in equation ($\ref{eq:3.3}$),

$$\begin{align*}\sin\delta_t &\approx \sin\delta_u + (\cos\delta_u)(\alpha)\cos A\\ \sin\delta_t - \sin\delta_u &\approx \alpha \cos\delta_u \cos A\\ 2\sin(\frac{\delta_t-\delta_u}{2})\cos(\frac{\delta_t+\delta_u}{2}) &\approx \alpha \cos\delta_u \cos A\end{align*}$$

and because $\delta_t \approx \delta_u$ (i.e. $|\delta_t - \delta_u| \ll 1$),

$$\begin{align*}2(\frac{\delta_t-\delta_u}{2})\cos \frac{2\delta_u}{2} &\approx \alpha \cos\delta_u \cos A\\ (\delta_t-\delta_u)\cos \delta_u &\approx \alpha \cos\delta_u \cos A\end{align*}$$

or, provided $\delta_u \ne \pm\pi/2$,

$$\delta_t \approx \delta_u + \alpha \cos A$$

which is equation ($\ref{eq:4.3}$).

Using $|\Delta\lambda| \ll 1$, $|\alpha| \ll 1$, and $\delta_t \approx \delta_u$ in equation ($\ref{eq:3.4}$)

$$\Delta\lambda \approx \frac{\alpha \sin A}{\cos\delta_u}\quad \text{for } \delta_u \ne \pm\pi/2$$i.e.,$$\lambda_t \approx \lambda_u + \frac{\alpha \sin A}{\cos\delta_u} \quad \text{for } \delta_u \ne \pm\pi/2$$

which is equation ($\ref{eq:4.4}$).

5 Dilution of precision and other sources of error

The use of a geomagnetic field sensor to determine the Azimuth angle $A$ has an inherent source of error because the magnetic field of the Earth is not precisely aligned to its polar-axis. However, this error can be corrected using the GPS reading, the global declination angle map, and the International Geomagnetic Reference Field model. This is already part of most navigation systems and implemented into smart phones. (See this, for instance.) Further work is required towards handling the errors inherent in the GPS coordinates of the user and is not covered here.

6. Determination of $R$ from $\delta$ and the GPS reference ellipsoid

The reference coordinate system used by GPS is defined by revision WGS 84 of the World Geodetic System standard. The coordinate origin is located at the Earth's centre of mass with the IERS Reference Meridian being the meridian of zero longitude. The surface is an oblate spheroid (ellipsoid) with a semi-major axis (equatorial radius) $a = 6378137.0$m and a semi-minor axis (polar radius) $b = 6356752.314245$m so that the inverse flattening $1/f = 298.257223563$.

Any point on the reference ellipsoid at a latitude $\delta$ then satisfies the (polar form of the) equation of the corresponding generating ellipse:$$R(\delta) = \left(ab\right)/\sqrt{(a\sin\delta)^2+(b\cos\delta)^2}$$This gives the distance $R(\delta)$ from the centre of the Earth for any point at latitude $\delta$ on the surface of the reference ellipsoid.